Spotlight
MEDIA
Rewind: Leaving NRI voters behind
www.telanganatoday.com | 16 April, 2024
The Intersection of Women’s Mental Health and Circadian Rhythms in a 24/7 World
www.womenshine.in | 12 April, 2024
FLAME UNIVERSITY’S
LIBERAL
EDUCATION
Our educational philosophy is rooted in the concept of Liberal Education. We believe that the real world does not function in isolation, and neither should knowledge. By interconnecting social sciences, humanities, physical sciences, business, design, natural sciences, fine & performing arts, communications management and computational sciences, we equip our students for an ever-changing new world. At FLAME, our students interact with various disciplines and are encouraged to address pressing world challenges through different perspectives. Our aim is to help them grow as critical thinkers and lifelong learners, as they lead purposeful lives, rather than just narrow professions. Therefore, we foster an environment that is personalised, participatory, and provides a transformational experience to aid in their personal and professional journeys.
YOUR JOURNEY WITH FLAME | RE-INVENTING LIBERAL EDUCATION. AGAIN.
We challenge what is known and believed about higher education. From re-inventing liberal education in India, to helping you chart your own unique career path; FLAME is not where you are, it is for who you are, and where you want to be.
Our multidisciplinary curriculum encourages you to explore what drives you and makes you unique. You can discover new avenues of growth and scout over 350 career combinations to make a place for yourself in the real world.
We not only focus on finding answers to glaring world challenges, but also on creating new knowledge. With seven fully functional research centres, you can explore several faculty-student research opportunities.
With a 11:1 student:faculty ratio our faculty will mentor you one-on-one, where you can learn from their real-world experiences, hard-won career knowledge, and other life experiences. We believe that these relationships will set you up for future success.
The beautifully designed, high-tech campus has carefully crafted spaces for recreation, collaboration, and sports. Differently-styled spaces provide students and teachers with the flexibility to create learning environments on-the-go.
Creative Thinkers, Passionate Doers
OUR COMMUNITY OF ACTIVE AND ACCOMPLISHED SCHOLARS

India's 2,000-rupee note to be withdrawn from circulation on Sep 30
Prof. Devendra Kumar Jain
Faculty of Finance
Learn more about Prof. Devendra Kumar Jain and his views on this topic, and more.

The Taiwan conundrum: India balancing trade, technology, and security amid Chinese belligerence
Prof. Roger Liu
Faculty of International Studies
Learn more about Prof. Roger Liu and his views on this topic, and more.

Slice-North East Small Finance Bank Merger: What Fintech Cos Should Take Note Of
Prof. Jaslene Bawa
Faculty of Finance
Learn more about Prof. Jaslene Bawa and her views on this topic, and more.

Meira Paibis: Manipuri women caught between violence and narratives
Prof. Melody Kshetrimayum
Faculty of Academic Writing
Learn more about Prof. Melody Kshetrimayum and her views on this topic, and more.

The Sociology of Gaming: An Examination of Online Gaming Communities and Their Influence on Social Interaction
Prof. Sairaj Patki
Faculty of Psychology
Learn more about Prof. Sairaj Patki and his views on this topic, and more.

Child Care Institutions in India: A Critical Wake-Up Call for Reform Amidst Crisis
Prof. Rachna Mishra
Faculty of Psychology
Learn more about Prof. Rachna Mishra and her views on this topic, and more.
OUR COMMUNITY OF DOERS

Stuti Banga
Learning and Thriving: Stuti Banga's Pioneering Journey to Professional Prosperity

Naman Saxena
On his way as a Digital Marketing Apprentice at Google, Naman Recalls his days at FLAME
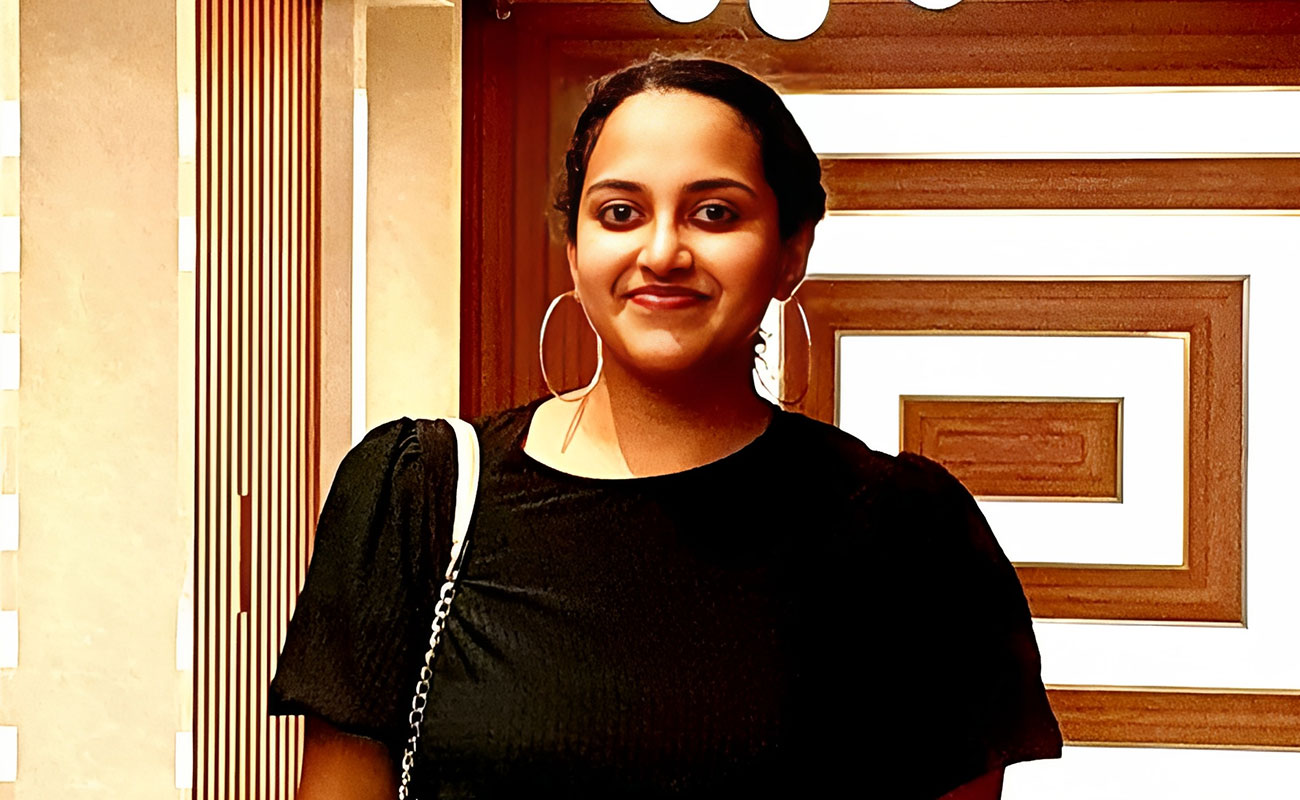
Dona Cherian
From Leo Burnett to Gulf News: Dona Cherian’s Journey of Passion and Impact
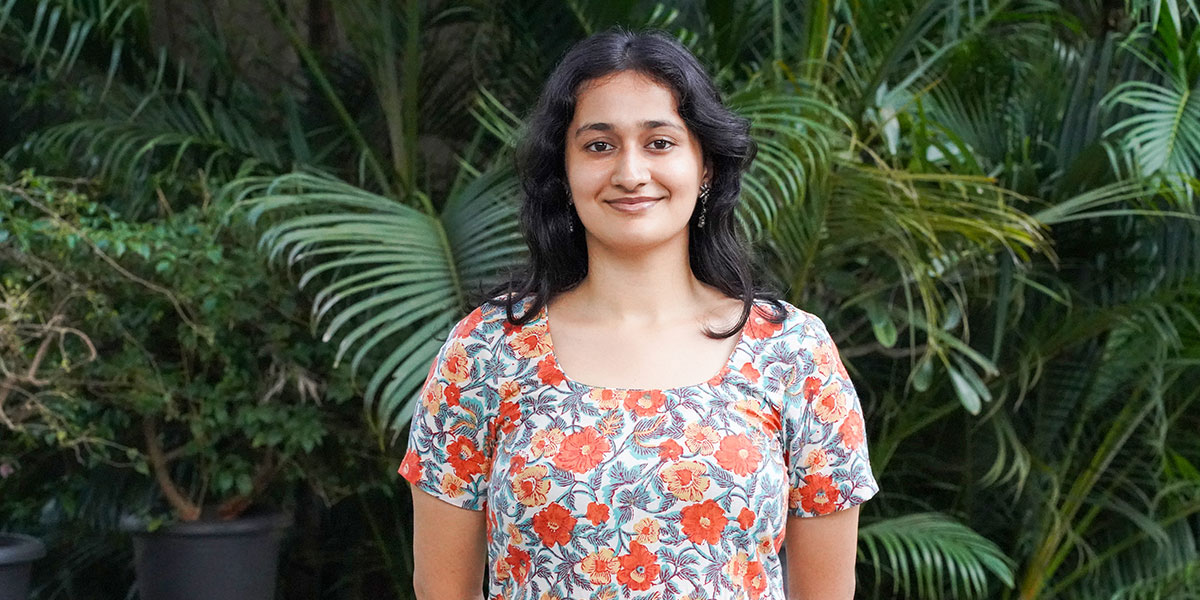
Sanvi Madan
Environmental Studies
Major
Public Policy Minor

Ayman Aboobacker
Entrepreneurship
Major
Design Minor


Taanya Malhotra
Major: Film & TV
Minor: Advertising & Branding

Vrinda Chokhani
Major: Finance
Minor: Economics

Aditya Ashok Balu
Major: International Studies
Minor: Environmental Studies

Rajvi Jhaveri
FLAME University
Semester abroad @Kelley School of Business
Dhriti Sumanth
FLAME University
Semester abroad @Wellesley College, USA

Manojna Lanka
FLAME University
Semester abroad @Wellesley College, USA
A TRANSFORMATIVE JOURNEY
PEOPLE, IMPACT, EXPERIENCES
Academics and a plethora of extra-curriculars. Research and exploration, for you and the world. Study groups and friend circles. Breaking boundaries and creating memories. Opening your mind and changing the world. FLAME helps you walk your path, on campus, and in the real world.
EXPLORE LIFE AT
Learn more about your FLAME experience, whether you're a student leader on the FLAME Student Council, rubbing elbows in Student Houses, learning through Peer and Faculty Mentoring, participating in Student Clubs, Exchange Programs, or Festivals.
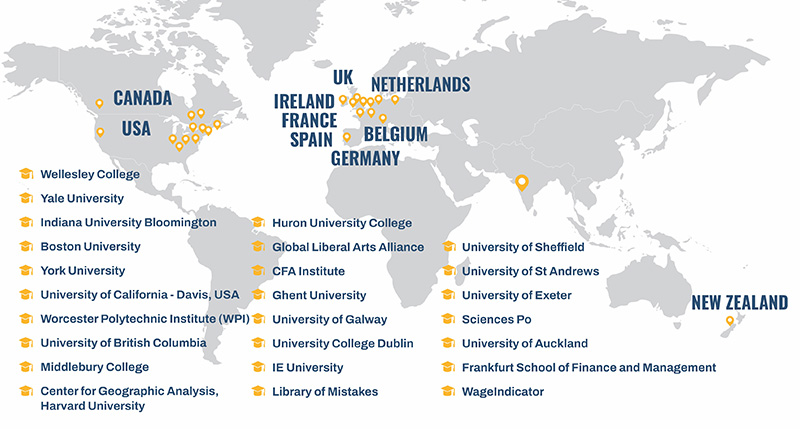
International Network
Connecting Worlds
Thinking, hearing, speaking, and teaching transcend borders. We help you navigate in a world that is influenced by many languages and diverse cultures, from a living to a learning experience. Consider learning internationally and take advantage of the world at your fingertips.
Learning Outside The Classroom
EXPERIENCE THE REAL WORLD
Change happens, but not just within a classroom. Apply your learnings and drive change through our exclusive real-world learning programs.
Stories from our community
Voice of FLAME
Join us as we celebrate the unique voices and diverse perspectives that make up our remarkable community.













































